Unechte Brüche verstehen lernen - Ein Kinderspiel!

Hast du dich jemals gefragt, was passiert, wenn der Zähler größer ist als der Nenner eines Bruchs? Dann bist du hier genau richtig! Wir tauchen ein in die Welt der unechten Brüche, auch bekannt als "uneigentliche Brüche". Keine Angst, es ist einfacher, als es klingt!

Brüche sind überall um uns herum, von der Pizza, die wir teilen, bis zu den Messungen beim Backen. Manchmal ist der obere Teil des Bruchs, der Zähler, größer als der untere Teil, der Nenner. Das nennt man einen unechten Bruch. In diesem Artikel erklären wir dir alles, was du darüber wissen musst, in einer kinderfreundlichen Sprache.

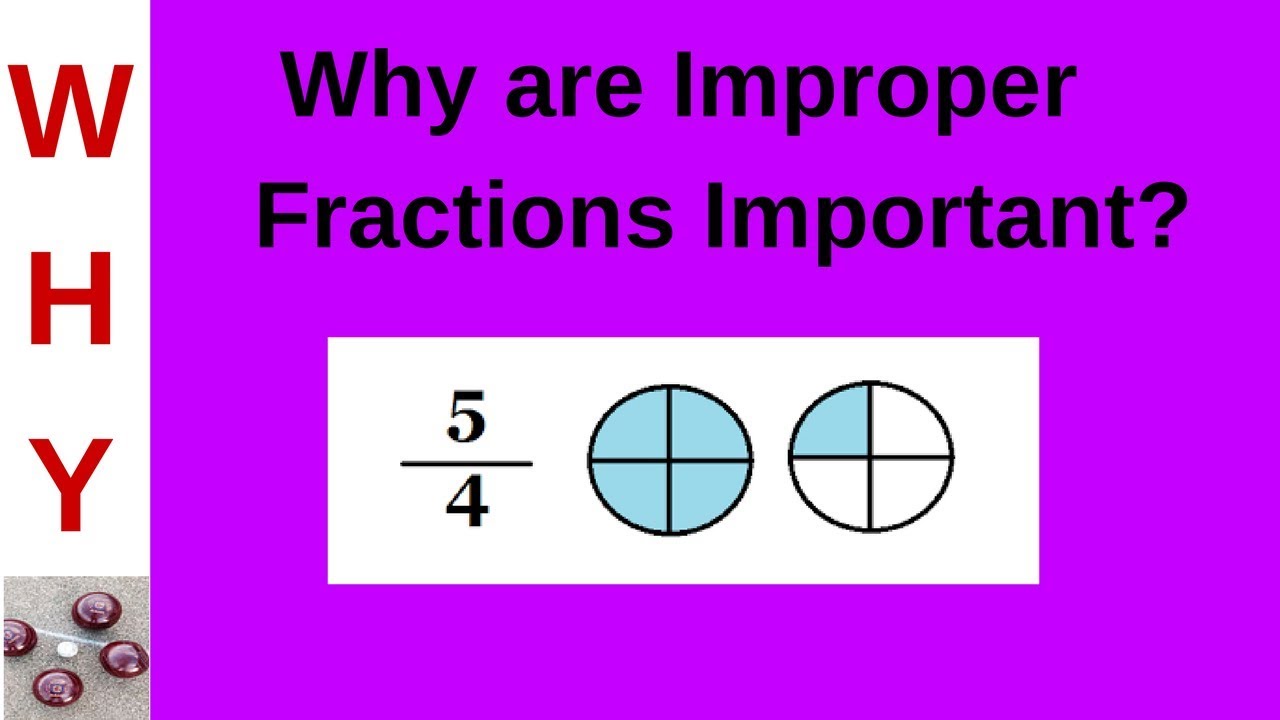
Stell dir vor, du hast zwei Pizzen, jede in vier Stücke geschnitten. Du isst insgesamt fünf Stücke. Wie drückst du das als Bruch aus? Du hast 5/4 gegessen – ein unechter Bruch! Die Erklärung für Kinder ist ganz einfach: Der Zähler (5) zeigt, wie viele Stücke du gegessen hast, und der Nenner (4) zeigt, in wie viele Stücke jede Pizza geschnitten wurde.

Das Verstehen von unechten Brüchen ist ein wichtiger Schritt im Bruchrechnen. Es hilft dir, Brüche zu addieren, zu subtrahieren, zu multiplizieren und zu dividieren, und bereitet dich auf komplexere mathematische Konzepte vor. Also, lass uns gemeinsam diese spannende Welt erkunden!

Dieser Artikel bietet eine umfassende Erklärung der Definition von unechten Brüchen für Kinder, einschließlich ihrer Geschichte, Bedeutung, Vor- und Nachteile, Beispiele und praktische Übungen. Wir werden auch häufige Fragen beantworten und hilfreiche Tipps und Tricks geben, um das Verständnis zu erleichtern.

Die Geschichte der Brüche reicht weit zurück in die Antike. Unechte Brüche sind ein natürlicher Bestandteil dieses Systems und entstanden aus der Notwendigkeit, Mengen darzustellen, die größer als ein Ganzes sind. Ihre Bedeutung liegt in ihrer Fähigkeit, Brüche und gemischte Zahlen ineinander umzuwandeln, was für viele mathematische Operationen unerlässlich ist.

Ein unechter Bruch ist ein Bruch, bei dem der Zähler (die obere Zahl) größer oder gleich dem Nenner (die untere Zahl) ist. Beispiele: 7/4, 11/3, 5/5. Ein einfacher Weg, sich das zu merken, ist: Der Zähler ist "uneigentlich" groß.

Vorteile von unechten Brüchen: Sie vereinfachen Berechnungen mit Brüchen, ermöglichen das Umrechnen in gemischte Zahlen und erleichtern das Verständnis von Verhältnissen.

Um einen unechten Bruch in eine gemischte Zahl umzuwandeln, teilt man den Zähler durch den Nenner. Der ganzzahlige Teil des Ergebnisses ist die ganze Zahl, der Rest ist der neue Zähler, und der Nenner bleibt gleich. Beispiel: 11/3 wird zu 3 2/3.

Häufig gestellte Fragen:

1. Was ist ein unechter Bruch? Antwort: Ein Bruch, bei dem der Zähler größer oder gleich dem Nenner ist.

2. Wie wandelt man einen unechten Bruch in eine gemischte Zahl um? Antwort: Teile den Zähler durch den Nenner. Der ganzzahlige Teil ist die ganze Zahl, der Rest ist der neue Zähler.

3. Warum sind unechte Brüche wichtig? Antwort: Sie vereinfachen Berechnungen mit Brüchen.

4. Sind alle Brüche mit gleichem Zähler und Nenner unechte Brüche? Antwort: Ja, z.B. 5/5.

5. Kann ein unechter Bruch kleiner als 1 sein? Antwort: Nein.

6. Ist 9/4 ein unechter Bruch? Antwort: Ja.

7. Ist 2/3 ein unechter Bruch? Antwort: Nein.

8. Wie addiert man unechte Brüche? Antwort: Man bringt sie auf den gleichen Nenner und addiert die Zähler.

Tipp: Übe das Umwandeln von unechten Brüchen in gemischte Zahlen und umgekehrt. Verwende visuelle Hilfsmittel wie Pizzen oder Kreise, um das Konzept zu veranschaulichen.

Zusammenfassend lässt sich sagen, dass unechte Brüche ein wichtiger Bestandteil des Bruchrechnens sind. Sie ermöglichen es uns, Mengen darzustellen, die größer als ein Ganzes sind, und vereinfachen viele mathematische Operationen. Das Verständnis von unechten Brüchen ist grundlegend für den weiteren Erfolg in der Mathematik. Nimm dir Zeit zum Üben und scheue dich nicht, Fragen zu stellen. Mit etwas Übung wirst du unechte Brüche im Handumdrehen meistern! Durch das Verständnis von unechten Brüchen legst du den Grundstein für komplexere mathematische Konzepte. Übung macht den Meister! Experimentiere mit verschiedenen Brüchen und visualisiere sie mit Alltagsgegenständen. So wird das Lernen zum Kinderspiel und du wirst schnell zum Bruch-Experten.

Herzliche mittwoch morgen grusse motivation und freude verschenken
Trost spenden mut machen kopf hoch
Geislinger zeitung digital nachrichten immer griffbereit